Angles
Table of Contents- Transformations
- Glossary
Geometry is a kind of math that studies the relationships between lines, shapes, and three-dimensional figures. Geometry is important to many jobs. Builders use geometry to figure out how much lumber and other material they need. Scientists use geometry to calculate formulas. People use geometry to figure out how much fencing to buy or how much paint they need to paint a room.
One part of geometry is the study of angles. An angle is made up of two rays. A ray is a part of a line. It starts at a point and extends forever from that point.

Two rays that have the same endpoint make an angle:

There are many kinds of angles. Angles sizes are measured in degrees (°). There are 360° in a full circle. We use a tool called a protractor to measure angles.

A right angle is 90°. It is a perfectly square corner like the corner of a piece of paper or the angle where two walls come together.

An acute angle is smaller than a right angle. It measures less than 90°.

An obtuse angle is larger than a right angle. It measures less than 90°.

A straight angle is made of two rays that make a straight line. It measures 180°.

We can use this information to estimate or guess the size of an angle. If an angle is smaller than a right angle, it must be less than 90°. It is larger than a right angle but less open than a straight line, it must be between 90° and 180°. If it is larger or more open than a straight line, then it must be larger than 180°.
Estimate the size of these angles:
1. 
2. 
3. 
4. 
Two angles that have measures that add to be 90° are called complementary angles. If you know the measure of one angle in a pair of complementary angles, you can figure out the measure of the other by subtracting from 90°.
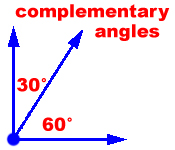
Two angles that have measures that add to be 180° are called supplementary angles. If you know the measure of one angle in a pair of supplementary angles, you can figure out the measure of the other by subtracting from 180°.

If two angles have the same measure, they are congruent.
When two lines cross or intersect, four angles are formed. The pairs of opposite angles are called vertical angles. Vertical angles always have the same measure. They are congruent.

In this diagram, angles A and C are vertical angles. They have the same measure. Angles B and D are also vertical angles. They are congruent.
A transversal is a line that crosses two parallel lines. Eight different angles are created by this line. Look at the angles and see which ones look like they are the same size.

There are four pairs of angles in this that are the same size. They are called corresponding angles.

Alternate angles also have the same size.

Here is a trick to help you remember this. If a line crosses two parallel lines, all the resulting angles will be one of two sizes. And the supplementary angles (above or below the parallel lines) will always add to 180°. Knowing this, you should be able to figure out how big all the angles are if you are given just one!
Now, let’s practice. Give the size of the angle marked.
5. 
6. 
7. 
8. 
Transformations
A transformation is a change in a shape, or a way of mapping the shape onto another space. Examples of transformations are slides, flips, and turns.
A translation, or slide, is moving a shape along a line. The shape is scooted over, like you’d slide a plate from one person to another. Here is an example of a translation:

A reflection, or flip, is a way of moving a shape across a line, producing a mirror image. It is like flipping a pancake. Here is an example of a reflection:

A rotation, or turn, s the turning or spinning a shape. It is like a person doing a cartwheel. Here is an example of a rotation:

A dilation is making a shape bigger or smaller. The shape stays the same, it is just blown up larger or shrunk down smaller.

Shapes that are congruent have the exact same shape and size. They could be slid, flipped, or turned and would then be exactly the same. These are examples of congruent shapes:

Shapes that are similar have the same shape, but may be different sizes. These are examples of similar shapes:

Now you can practice identifying transformations.
9. 
A) translation
B) reflection
C) rotation
D) dilation
10. 
A) translation
B) reflection
C) rotation
D) dilation
11. 
A) translation
B) reflection
C) rotation
D) dilation
12. 
A) translation
B) reflection
C) rotation
D) dilation
Glossary
alternate angles – two congruent angles on the opposite side of a transversal that border different parallel lines
angle – a figure formed from two rays extending from the same point
bisect – to divide into two equal parts
complementary angles – two angles that add up to 90°
congruent – having the same shape and same size
corresponding angles – two congruent angles on the same side of a transversal that border different parallel lines
dilation – an enlargement or reduction of a figure
geometry – a field of math that studies the relationships between lines, shapes, and three-dimensional figures
opposite angles – two angles that don’t touch each other and are formed by crossing lines; also called vertical angles
parallel – lines that are exactly the same distance apart and would never meet
perpendicular – at a right angle; at 90° to something
ray – a line extending indefinitely from a single point
reflection – a flip of a figure; a movement of a figure across a line, producing a mirror image
rotation – turn; the turning of a figure
supplementary angles – two angles that add up to 180°
transformation – a change in a shape, or a way of mapping the shape onto another space; examples: translation, reflection, rotation
translation – slide; to move a figure along a line
transversal – a line that divides two parallel lines
vertical angles – two angles that don’t touch each other and are formed by crossing lines; also called opposite angles

